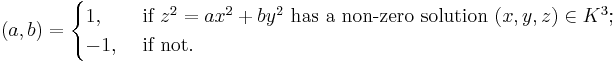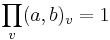Hilbert symbol
In mathematics, given a local field K, such as the fields of reals or p-adic numbers, whose multiplicative group of non-zero elements is K×, the Hilbert symbol is an algebraic construction, extracted from reciprocity laws, and important in the formulation of local class field theory. As the name suggests, it was in some sense introduced by David Hilbert, although it would be anachronistic to say that of the local field formulation.
Explicitly, it is the function (–, –) from K× × K× to {−1,1} defined by
Contents |
Properties
The following three properties follow directly from the definition, by choosing suitable solutions of the diophantine equation above:
- If a is a square, then (a, b) = 1 for all b.
- For all a,b in K×, (a, b) = (b, a).
- For any a in K× such that a−1 is also in K×, we have (a, 1−a) = 1.
The (bi)multiplicativity, i.e.,
- (a, b1b2) = (a, b1)·(a, b2)
for any a, b1 and b2 in K× is, however, more difficult to prove, and requires the development of local class field theory.
The third property ensures that the Hilbert symbol factors over the second Milnor K-group 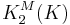 , which is by definition
, which is by definition
- K× ⊗ K× / (a ⊗ 1−a, a ∈ K× \ {1})
By the first property it even factors over 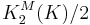 . This is the first step towards the Milnor conjecture.
. This is the first step towards the Milnor conjecture.
Interpretation as an algebra
The Hilbert symbol can also be used to denote the central simple algebra over K with basis 1,i,j,k and multiplication rules 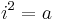 ,
, 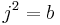 ,
, 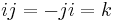 . In this case the algebra represents an element of order 2 in the Brauer group of K, which is identified with -1 if it is a division algebra and +1 if it is isomorphic to the algebra of 2 by 2 matrices.
. In this case the algebra represents an element of order 2 in the Brauer group of K, which is identified with -1 if it is a division algebra and +1 if it is isomorphic to the algebra of 2 by 2 matrices.
Hilbert symbols over the rationals
For a place v of the rational number field and rational numbers a, b we let (a, b)v denote the value of the Hilbert symbol in the corresponding completion Qv. As usual, if v is the valuation attached to a prime number p then the corresponding completion is the p-adic field and if v is the infinite place then the completion is the real number field.
Over the reals, (a, b)∞ is +1 if at least one of a or b is positive, and −1 if both are negative.
Over the p-adics with p odd, writing 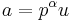 and
and 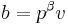 , where u and v are integers coprime to p, we have
, where u and v are integers coprime to p, we have
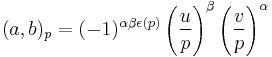 , where
, where 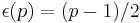
and the expression involves two Legendre symbols.
Over the 2-adics, again writing 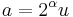 and
and 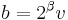 , where u and v are odd numbers, we have
, where u and v are odd numbers, we have
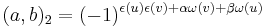 , where
, where 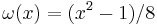 .
.
It is known that if v ranges over all places, (a, b)v is 1 for almost all places. Therefore the following product formula
makes sense. It is equivalent to the law of quadratic reciprocity.
External links
References
- Z. I. Borevich, I. R. Shafarevich (1966), Number theory, Academic Press, ISBN 0-12-117851-X
- Milnor, John Willard (1971), Introduction to algebraic K-theory, Annals of Mathematics Studies, 72, Princeton University Press, MR0349811
- Vostokov, S. V.; Fesenko, I. B. (2002), Local fields and their extensions, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-3259-2, http://www.maths.nott.ac.uk/personal/ibf/book/book.html
- Serre, Jean-Pierre (1996), A Course in Arithmetic, Graduate Texts in Mathematics, 7, Berlin, New York: Springer-Verlag, ISBN 978-3-540-90040-5